Modelization of filtration flows across thin membranes
Filtration across permeable surfaces is massively employed in industrial processes such as desalination, sterile filtration, food processing, and other medical and environmental applications like fog water harvesting systems. In Nature, Aquaporins porous membranes of biological cells which enables for water transport between cells are crucial in uncountable organisms. These processes typically involve two distinct length scales, the first related to the macroscopic size of the membrane, and the second to the length of the pores composing the membrane, ranging from nanometers to millimeters. The comprehensive understanding and predictive modeling of these separation processes are of great interest for technological progress. Here, in collaboration with the research group led by Dr. G.A. Zampogna, we exploit homogenization theory to develop large-scale boundary conditions which faithfully reproduce the transport across thin membranes. The resulting model, so-called Effective Concentration Jump Model, allows one to reproduce the macroscopic behavior of the flow across a wide range of phoretic conditions, involving non-reacting, chemostat and partially absorgind/desorbing walls composing the pores of the membrane. As reported in panel (a), the separation of scales allows for a inner and outer asymptotic expansions which, upon asymptotic matching, leads to a concentration boundary condition coupled with the pure hydrodynamic problem, developed by Dr. Zampogna in a previous work. The comparison with full-scale simulations depicts a very good agreement with the upscaled model.
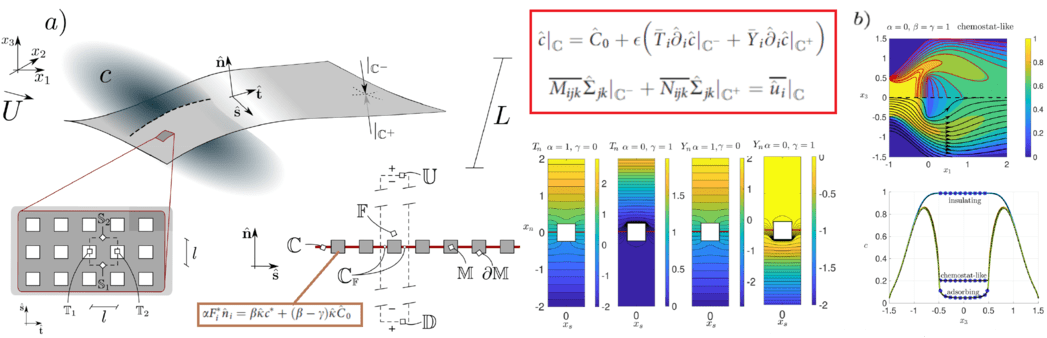
When dealing with Janus membranes, i.e. thin permeable structures with chemical and geometrical asymmetric properties, relevant variations of the chemical properties occur at the membrane thickness scale. To capture these fast variations, we leverage homogenization theory to capture such macroscopic discontinuities through a jump in the velocity and concentration fields of solvent and solute, respectively.Upstream and downstream spatial averages are introduced to account for discontinuities induced by the microstructure. The homogenized model quantifies the macroscopic jump, across the membrane, in the solvent velocity and stresses, and in the solute concentration and fluxes through coefficients obtained via closure problems at the micro-scale. The model paves the way towards a better understanding of fundamental interface phenomena such as osmosis and phoresis via homogenization.
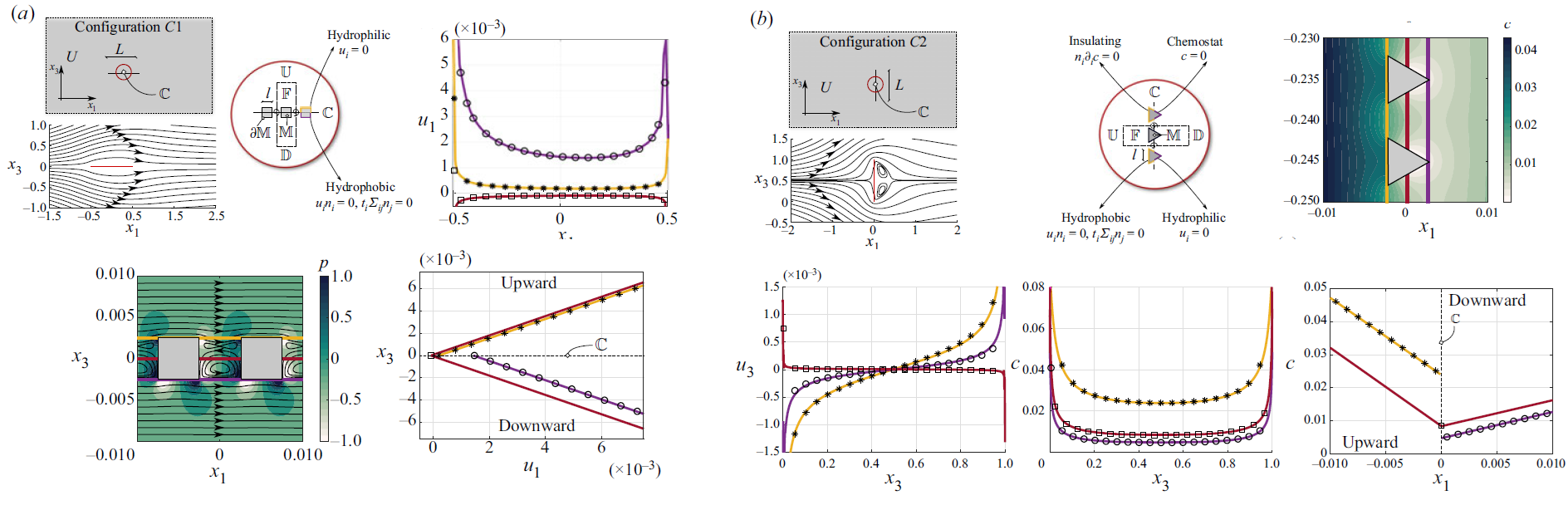
Next developments will include the full-coupling between solute and solvent fluxes (i.e. osmosis) and the generalization to higher Reynolds and Peclet numbers flows, to ensure the possibility to describe relevant industrial filtration processes involving water.